The long tail of the epidemic
Thankfully, the measures taken to reduce the transmission of the coronavirus seem to work. In Germany (and elsewhere) we're seeing a discussion on lifting restrictions. It would be good to inform the discussion with some quantitative picture of the trade-off here.
Time to get the maths out again. Also the usual disclaimer: I'm a mathematician and modeller, not an epidemiologist.It turns out that the professionals tend to agree.
So today, the scare word of the day was "Öffnungsdiskussionsorgien" used by Angela Merkel to deride the demands to "go back to normal" all to soon. Whether or not this was hyperbole, it seems we can adapt the old saying to Reopen in haste, repent at leisure.
To add some perspective to the situation: I was happy to see head of the German chancellery Helge Braun stated in an interview that "herd immunity" (without a vaccine) is not a viable strategy. The argument given was not based around the death toll that would take (which is severe), but that when staying within the presumed medical system capacity, it would take years to achieve. We saw last time that it would also be a dance on a very narrow grate with a reproduction number of $R > 1.2$ or so meaning overload of the health care system and $R<1$ meaning not reaching herd immunity.
So no herd immunity. And that we want to avoid $R>1$ is agreed on.
But what could be a goal? Let us make an example: We currently do not seem to have a plan how to reopen schools and Kindergarten, especially for the younger kids aside from a curious focus on the senior year students. They need to learn to read and write and calculate, the idea of reopening is dismissed with the comment that they cannot keep to the distancing and hand-washing as well as adults.There actually is some discussion how much schoolchildren contribute to the spread of the disease. Given that they are mostly asymptomatic and there is quite a bit of evidence that asymptomatic cases are less contagious, it seems frivolous to assume they do as much as adults and publish alarmist studies to get the attention you never get with modelling traffic jams. Some infectologists believe that children spread the virus much less.
What I see missing from the discussion is that even when disregarding the possibility of $R$ going above $1$ again, the trade-off is drastic in terms of opportunity cost.
Let's make some assumptions:
- We start at about $4000$ new cases per day. We'll disregard reported/non-reported for this.
- We assume that we might be able to trace $100$ new cases per day.
- We can open Schools and Kindergarden when reaching $\leq 100$ new cases per day.
Now, the key number discussed here is again the reproduction number $R$, the number of people in infected person in turn infects (when all of the contacts are susceptible, i.e. not yet immune) over the course of their illness.
But we need another number, the serial interval $S$, the average time between successive cases in an infection chain, i.e. the onset of illness in one person and the onset of illness in people they infected. The RKI gives an estimate of around 4.
This gives us the opportunity to investigate the development of the number of infections: Taking the number $I_{new}$ of new cases per day, we now know that each new case at $t$ will lead to R cases at $t + S$ (we ignore that the actual time between infections is stochastic).
Assuming things go smoothly in between, we have $$I_{new}(t) = I_{new}(0) R^{t/S}.$$
But now we can study what various levels of $R$ mean when we can reopen schools!
Setting $I_{new}(t) = 100$ and solving for $t$ we get
$$t_{100} = S \frac{\ln(100 / I_{new}(0))}{\ln R}$$.
We can also make a graph of the development:
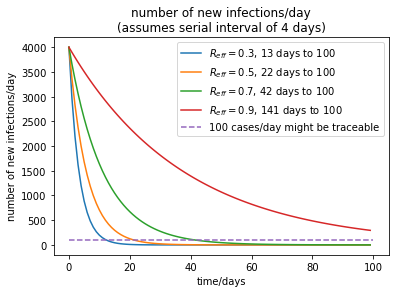
We see that at $R=0.3$ it only takes $22$ days to go from 4000 new infections per day to 100. With $R=0.5$ it takes $22$ days and with the recent RKI estimate of $R=0.7$ it takes $42$. If $R$ goes up to $0.9$, we would have to wait $141$ days.I rounded the number of days to the next larger integer.
Keep in mind that the exact numbers depend on the assumptions we made above. We can, however, see that the lower $R$ is, the better, and even a modest change in $R$ means that we are a lot better or worse off.
What have we learnt? The more we open up now and the more we allow the reproduction number $R$ to move up, the longer anything we are not opening up now will need to stay closed.
Do we value kids going to school soon again? Do we really want to delay that for being able to watch soccer on TV?Don't get me started on the fact that the very same people that now want to open this and that very urgently - thereby delaying the return to school - told kids that skipping school to demonstrate for more decisive action to keep larger parts of the planet sanely habitable were making a bad trade-off.
Reopen in haste, repent at leisure, indeed.
I should say that fewer total infections are a goal in itself, but this is generally understood. What I think is largely undervalued is that "return to as normal as possible" will be much quicker if we manage to keep the reproduction number low for a bit longer.